Numerical methods

We are developing numerical methods for the solution of linear, non-linear, and eigenvalue problems. Though we have primarily applied these techniques in DFT, they are applicable to a variety of fields

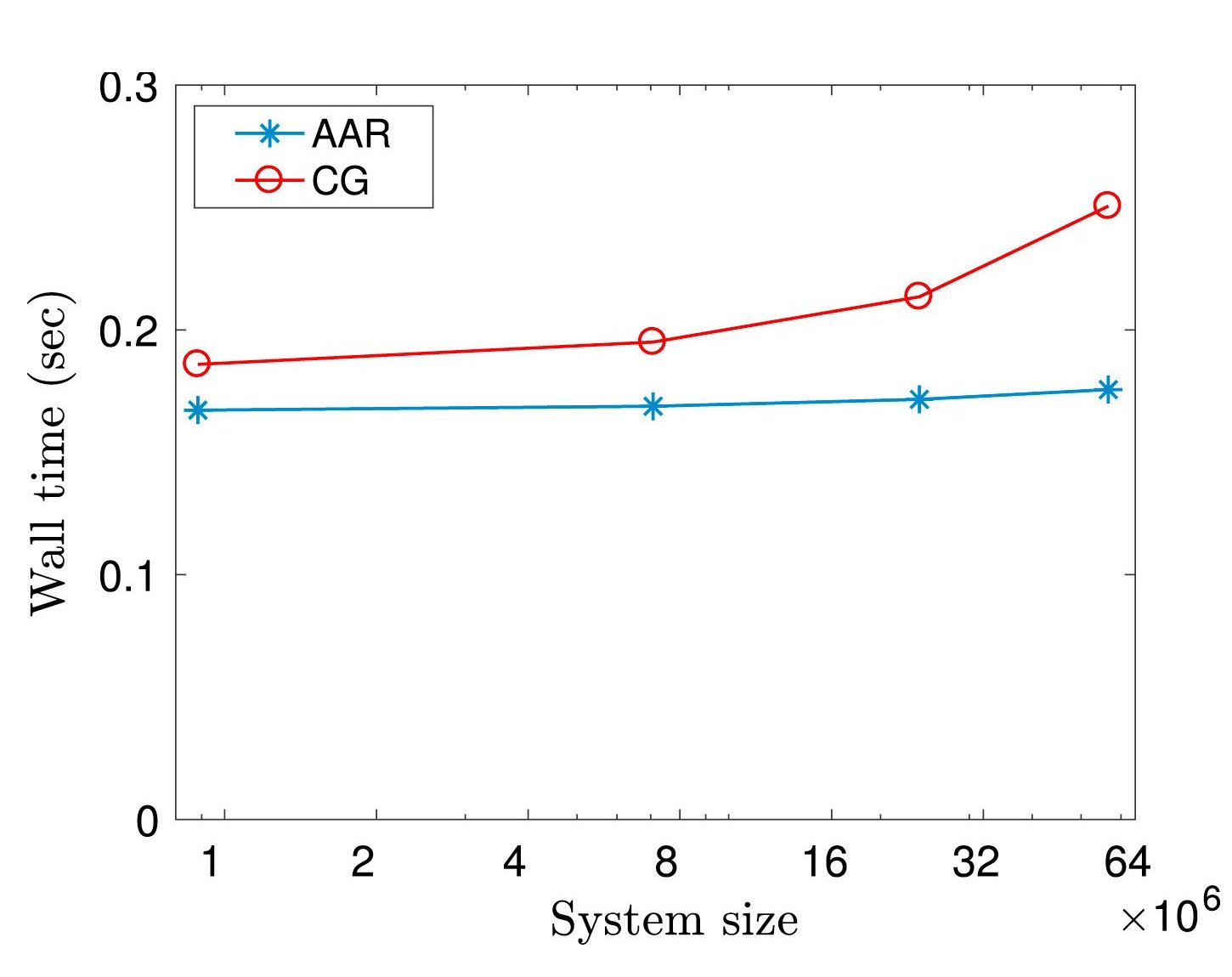
• Alternating Anderson-Richardson (AAR) method: We have developed the Alternating Anderson-Richardson (AAR) method: an efficient and scalable alternative to preconditioned Krylov solvers for the solution of large, sparse linear systems on high performance computing platforms [AAR1, AAR2]. AAR is equally applicable to symmetric as well as non-symmetric linear systems and does not make any assumption regarding the spectrum of the coefficient matrix. Overall, AAR offers a robust and efficient alternative to current state-of-the-art solvers, with increasing advantages as the number of processors grows. Analogous solvers have applications in other fields for accelerating linear fixed-point iterations.


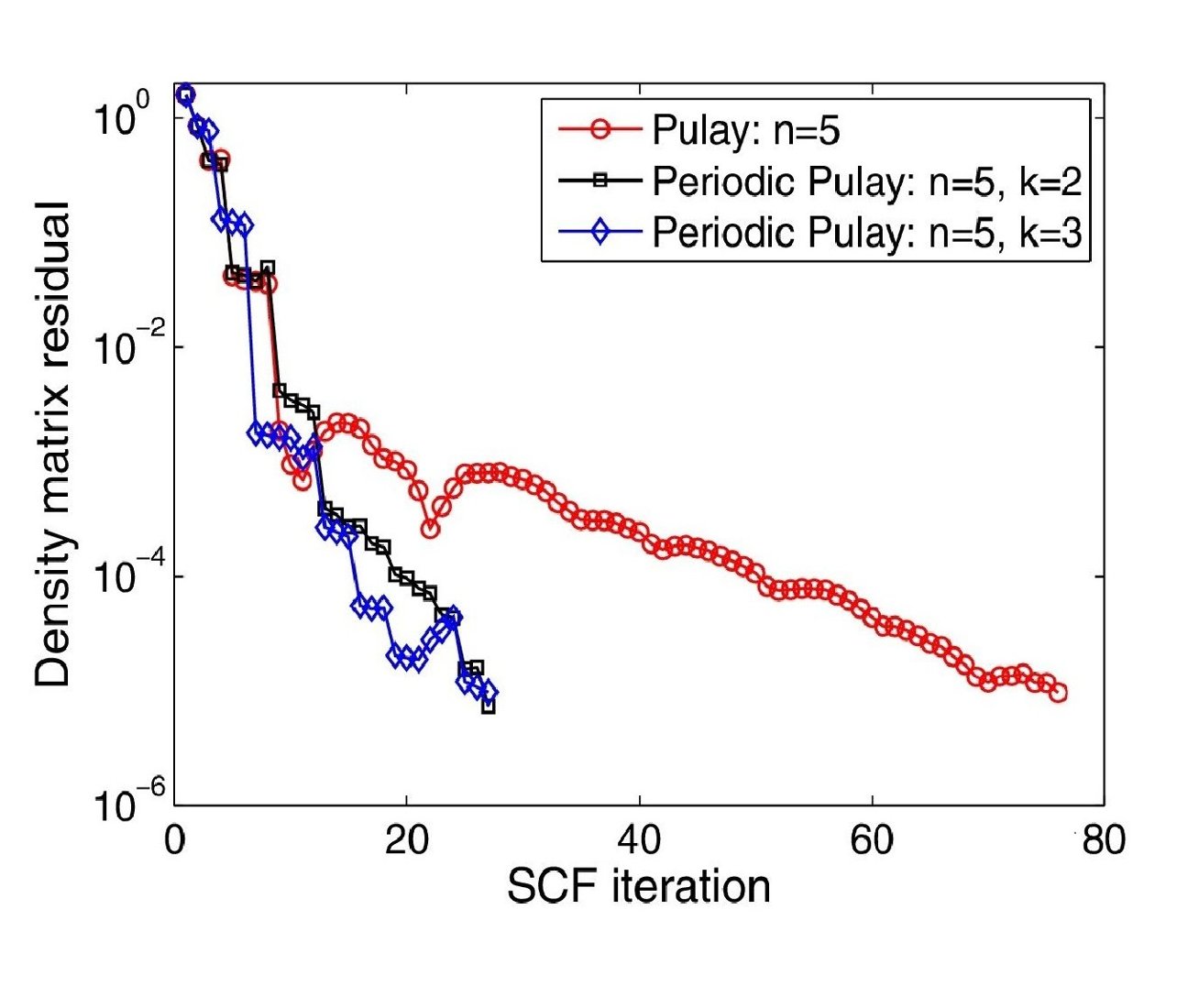
• Periodic Pulay and r-Pulay methods: Pulay's Direct Inversion in the Iterative Subspace (DIIS) method is one of the most widely used mixing schemes for accelerating the self-consistent solution of electronic structure problems. We have developed the Periodic Pulay method [PP], which represents a simple generalization of DIIS in which Pulay extrapolation is performed at periodic intervals rather than on every self-consistent field iteration, and linear mixing is performed on all other iterations. We have also developed an efficient way to introduce restarts within the Pulay method, which we refer to as the r-Pulay method [r-Pulay]. Overall, we have found that Periodic Pulay and r-Pulay are significantly more efficient and robust compared to the Pulay method. Analogous solvers have applications in other fields for accelerating nonlinear fixed-point iterations.


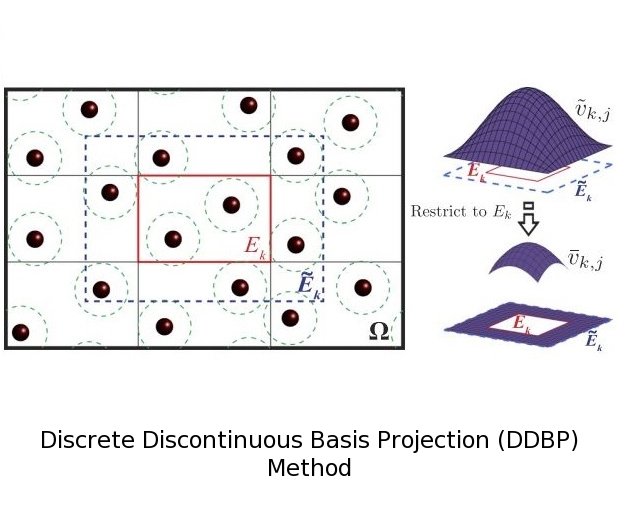
• Discrete Discontinuous Basis Projection (DDBP) method: The DDBP approach [DDBP] to accelerate real-space electronic structure methods several fold, without loss of accuracy, by reducing the dimension of the discrete eigenproblem that must be solved. In DDBP, we construct an efficient, systematically improvable, discontinuous basis spanning the occupied subspace and project the real-space Hamiltonian onto the span. Accurate energies and forces are obtained with 8–25 basis functions per atom, reducing the dimension of the associated real-space eigenproblems by 1–3 orders of magnitude. Analogous solvers have applications in other fields for solving large, sparse eigenproblems.