Research

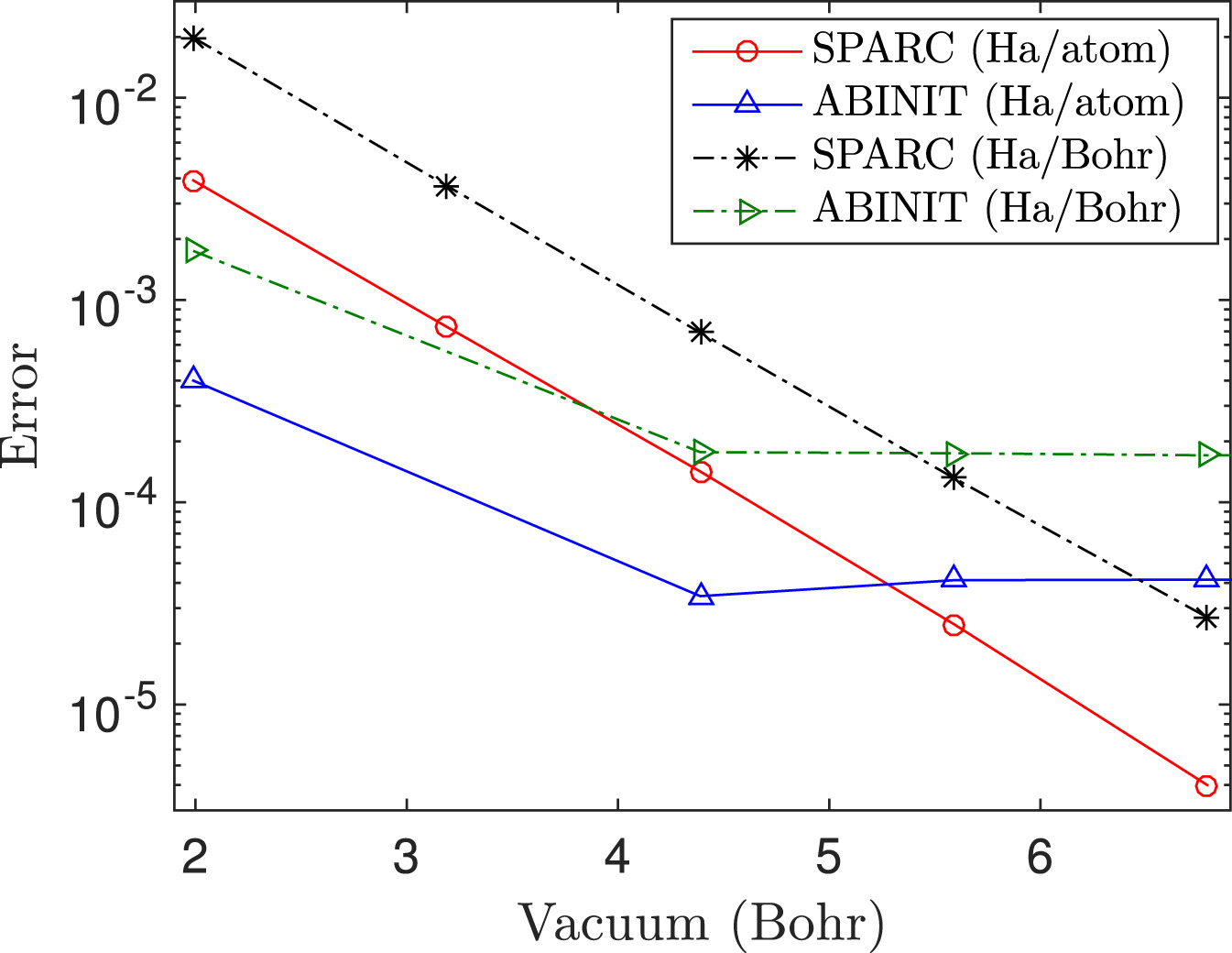
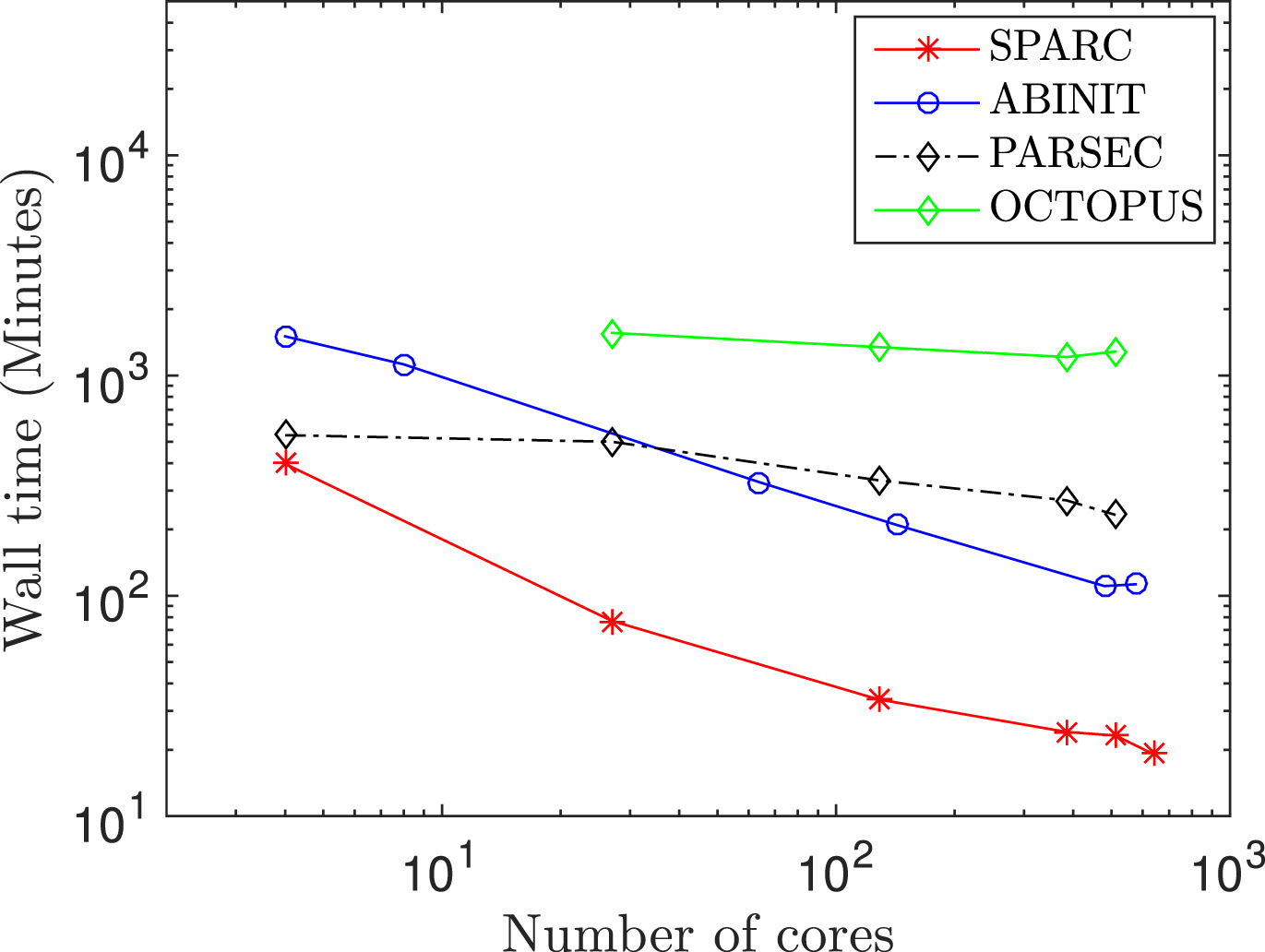
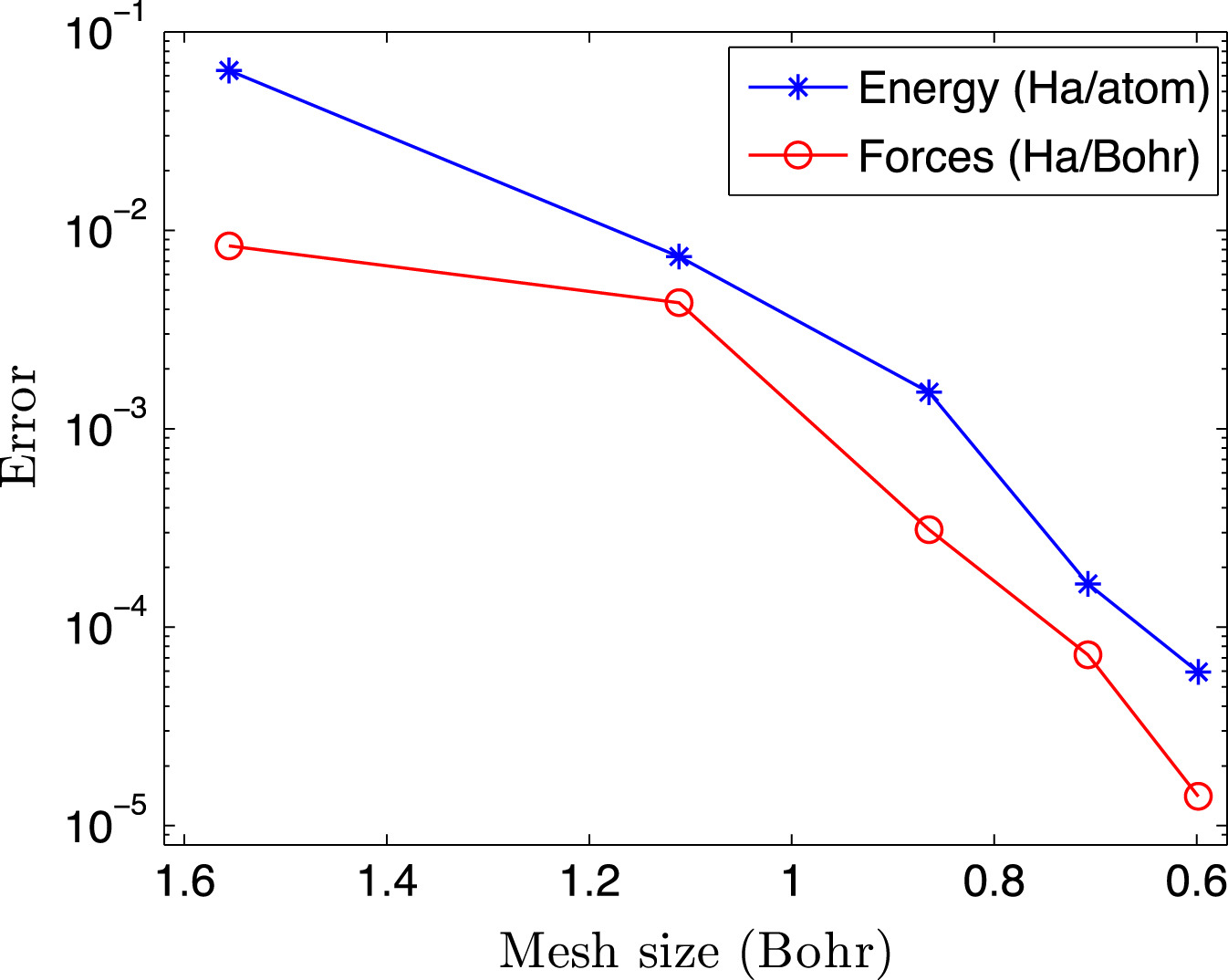
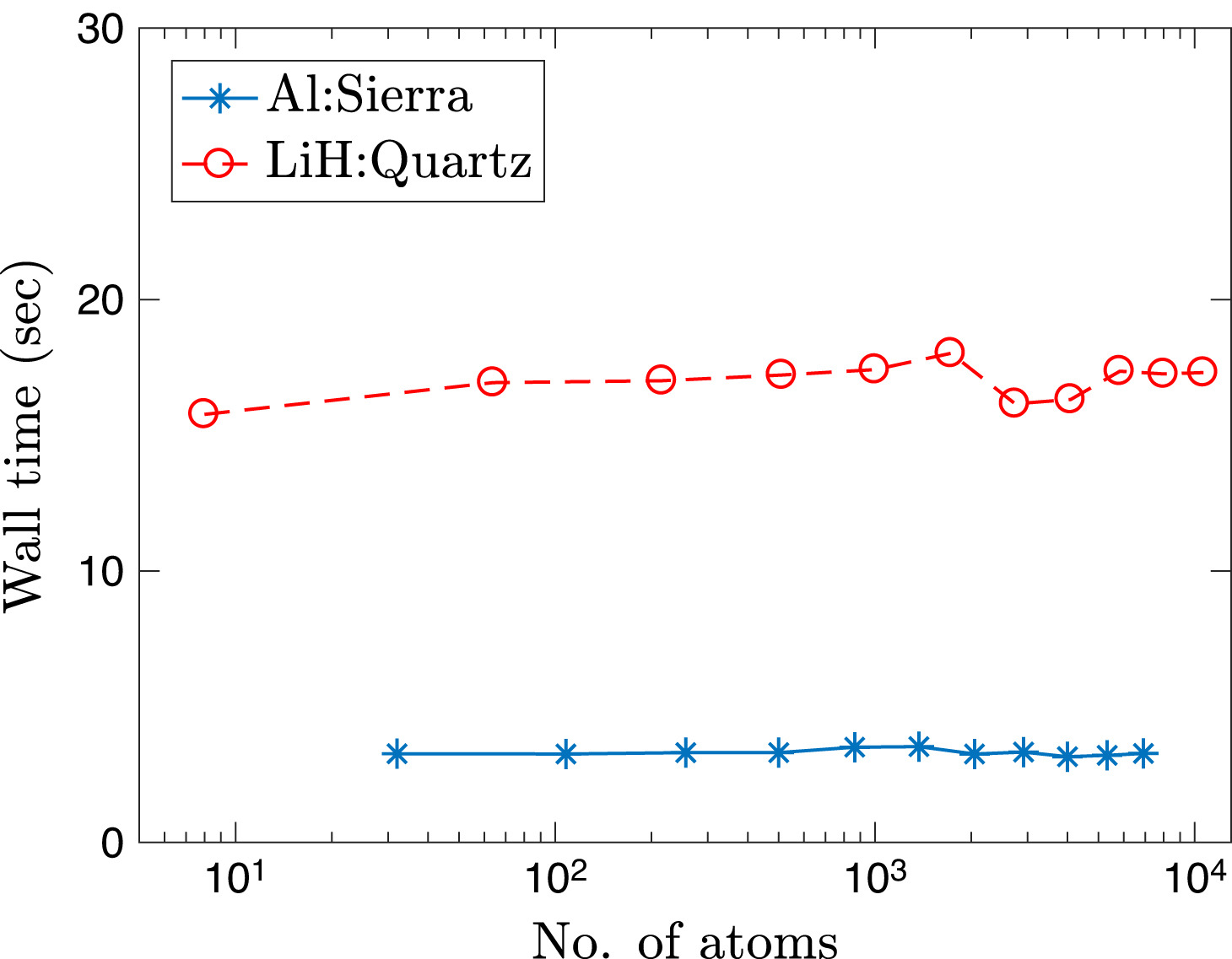
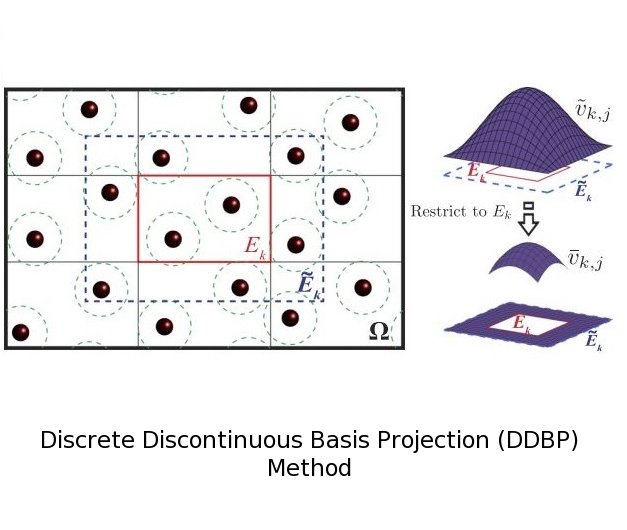
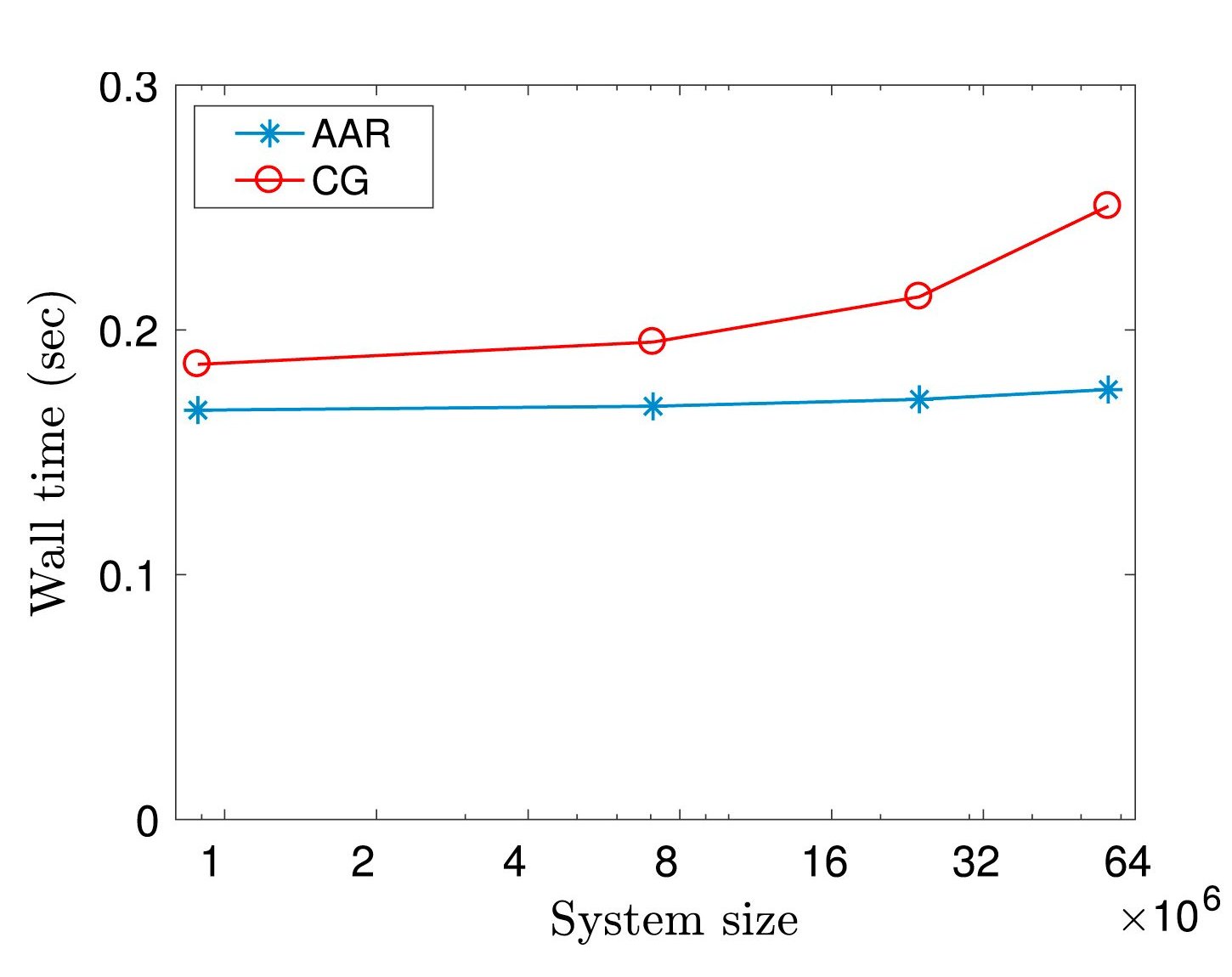
Ⅰ. Simulation Package for Ab-initio Real-space Calculations at Extreme Scales

Traditional methods for DFT utilize the plane-wave basis. However, the non-locality of plane-waves makes them unsuitable for the development of approaches that scale linearly with respect to the number of atoms. Furthermore, developing parallel implementations that can efficiently utilize large-scale computer architectures is challenging. Finally, the need for periodic boundary conditions limits their effectiveness in the study of non-periodic and localized systems such as defects, as well as non-traditional symmetries like cyclic and helical. To overcome these limitations, we have developed a new real-space formulation and parallel implementation of DFT referred to as SPARC [SPARC1, SPARC2], which is highly competitive with plane-wave codes that have been developed by large teams of researchers over a couple of decades. SPARC has the potential to significantly impact a number of other fields including mechanics, materials science, physics, and chemistry, as evidenced by the fact that a large fraction of the world's computational resources are used for performing DFT calculations. Current efforts to extend the capabilities and performance of SPARC—the resulting framework is referred to as SPARC-X—with applications to catalysis, can be found here.

Ⅱ. O(N) Ab-initio framework for materials under extreme conditons

In order to overcome the critical cubic-scaling bottleneck with respect to system size, much research in the past two decades has been devoted to the development of linear-scaling solution strategies for DFT. Rather than calculate the orthonormal Kohn-Sham orbitals, these techniques directly determine the quantities of interest with linear-scaling cost by exploiting the nearsightedness of matter. Though these efforts have yielded significant advances, there are a number of limitations. In particular, the accuracy and stability of linear-scaling methods remain ongoing concerns due to the need for additional computational parameters, subtleties in determining sufficient numbers and/or centers of localized orbitals, limitations of underlying basis sets, and calculation of accurate atomic forces, as required for structural relaxation and molecular dynamics simulations. In addition, efficient large-scale parallelization poses a significant challenge due to complex communications patterns and load balancing issues. Finally, and perhaps most importantly, the assumption of a band gap in the electronic structure makes these methods inapplicable to metallic systems.

High temperature calculations present additional challenges for DFT. These include the need for a significantly larger number of orbitals to be computed, as the number of partially occupied states increases, and need for more diffuse orbitals, as higher-energy states become less localized. Consequently, cubic-scaling methods as well as local-orbital based linear-scaling methods have very large prefactors, which makes them unsuitable for the study of materials under extreme conditions. In order to overcome these limitations, in the framework provided by the SPARC formulation and implementation, we have recently developed a linear-scaling DFT formulation and implementation referred to as SQDFT [SQDFT1, SQDFT2, SQDFT3], whose cost actually decreases with increasing temperature. Furthermore, it can efficiently scale up to a hundred thousands computational processors, and is therefore able to simulate systems whose sizes are two orders of magnitude larger than previously feasible. SQDFT is currently being utilized to study a variety of materials systems at extreme conditions.

Ⅲ. Ab-initio framework for systems with non-traditional symmetries

Nanostructures have tremendous number of applications, including energy harvesting, efficient power transmission, curing terminal diseases, and design of materials with high specific strength. Therefore, the development of techniques that enable the systematic design and discovery of novel nanostructures with tailored properties is of tremendous interest. Unfortunately, current experimental approaches are generally time consuming, expensive and typically rely on empirical insight. Further, accurate computational techniques like DFT are unable to characterize complex nanostructures and systematically traverse the enormous configurational space because of their large computational expense. This is mainly a consequence of their inability to exploit non-traditional symmetries that are typically present in nanostructures displaying exotic and novel properties. In order to overcome this, in the framework provided by SPARC, we are currently developing a novel DFT framework that is compatible with all the symmetry groups, which will not only provide tremendous simplification in the characterization of nanostructures, but will also accelerate the design of new nanostructures by allowing the use of symmetry to parameterize the configurational space of nanostructures.

As first steps towards achieving this goal, we have developed Cyclic DFT [Cyclic I, Cyclic II] and Helical DFT in the framework provided by the SPARC formulation, which can exploit the cyclic and helical symmetries present in the system to tremendously reduce the computational cost. Since uniform bending deformations can be associated with cyclic symmetry and uniform torsional deformations can be associated with helical symmetry, Cyclic and Helical DFT provide an elegant route to the ab-initio study of bending and torsion in nanostructures. Ab-initio simulations of this nature are unprecedented and well outside the scope of any other systematic first principles method in existence. For example, Cyclic DFT was recently employed to study the properties of a 2 micron sized nanostructure, which is two orders of magnitude larger than state-of-the-art. Cyclic and Helical DFT are currently being used to study the interaction of mechanical deformations with electric and magnetic fields in nanostructures.

Ⅳ. Ab-initio framework for the study of crystal defects

Crystal defects, though present in relatively minute concentrations, play a significant role in determining material properties. This necessitates an accurate characterization of defects at physically relevant defect concentrations (parts per million), which represents a unique challenge since both the electronic structure of the defect core as well as the long range elastic field need to be resolved simultaneously. Since routine DFT calculations are limited to hundreds of atoms, this represents a truly challenging open problem. In order to solve this, we have developed a method to coarse-grain DFT that is solely based on approximation theory, without the introduction of any new equations and resultant spurious physics [CGDFT1]. This work has opened an avenue for the study of extended crystal defects using DFT, which represents a vital step towards understanding the deformation and failure mechanisms in solids. We are currently utilizing this framework to characterize dislocations, the interactions between them, and their interaction with macroscopic fields (e.g. strain).

Ⅴ. Numerical methods

We are developing numerical methods for the solution of linear, non-linear, and eigenvalue problems. Though we have primarily applied these techniques in DFT, they are applicable to a variety of fields

• Alternating Anderson-Richardson (AAR) method: We have developed the Alternating Anderson-Richardson (AAR) method: an efficient and scalable alternative to preconditioned Krylov solvers for the solution of large, sparse linear systems on high performance computing platforms [AAR1, AAR2]. AAR is equally applicable to symmetric as well as non-symmetric linear systems and does not make any assumption regarding the spectrum of the coefficient matrix. Overall, AAR offers a robust and efficient alternative to current state-of-the-art solvers, with increasing advantages as the number of processors grows. Analogous solvers have applications in other fields for accelerating linear fixed-point iterations.


• Periodic Pulay and r-Pulay methods: Pulay's Direct Inversion in the Iterative Subspace (DIIS) method is one of the most widely used mixing schemes for accelerating the self-consistent solution of electronic structure problems. We have developed the Periodic Pulay method [PP], which represents a simple generalization of DIIS in which Pulay extrapolation is performed at periodic intervals rather than on every self-consistent field iteration, and linear mixing is performed on all other iterations. We have also developed an efficient way to introduce restarts within the Pulay method, which we refer to as the r-Pulay method [r-Pulay]. Overall, we have found that Periodic Pulay and r-Pulay are significantly more efficient and robust compared to the Pulay method. Analogous solvers have applications in other fields for accelerating nonlinear fixed-point iterations.


• Discrete Discontinuous Basis Projection (DDBP) method: The DDBP approach [DDBP] to accelerate real-space electronic structure methods several fold, without loss of accuracy, by reducing the dimension of the discrete eigenproblem that must be solved. In DDBP, we construct an efficient, systematically improvable, discontinuous basis spanning the occupied subspace and project the real-space Hamiltonian onto the span. Accurate energies and forces are obtained with 8–25 basis functions per atom, reducing the dimension of the associated real-space eigenproblems by 1–3 orders of magnitude. Analogous solvers have applications in other fields for solving large, sparse eigenproblems.